卡诺图在数字电路教学中的灵活运用

　字电子技术中，卡诺图是用最小项方格表示逻辑函数的方法，用图形表示输入变量与函数之间的逻辑关系。它用几何位置上的相邻，形象地表示了组成逻辑函数的各个最小项之间在逻辑上的相邻性。在教学中，卡诺图的学习是由化简逻辑函数引入的，所以初学者往往以为卡诺图只是数字分析和设计中用以化简逻辑函数的一种工具。其实不然，实际上灵活运用卡诺图，可以使逻辑电路的分析和设计过程大为简化，让一些难题迎刃而解。

 

　当函数间进行逻辑运算时，其卡诺图有如下特性：

　1．两个函数进行与运算时，只要画出两个函数的卡诺图，再将两个函数卡诺图中对应的方格相与，便得到这两个函数相与的卡诺图。

　2．两个函数进行或运算时，只要画出两个函数的卡诺图．再将两个函数卡诺图中对应的方格相或，便得到这两个函数相或的卡诺图。

　3．对于一个函数．只需将该函数卡诺图中的l格变为o格．0格变为l格，便得到该函数的反函数的卡诺图。

　由此可见，利用卡诺图对函数进行逻辑运算简单、明了。若对复杂的逻辑函数化简时，如果我们借助于卡诺图进行逻辑函数运算，可以伸复杂函数的化简讨程得以简化．

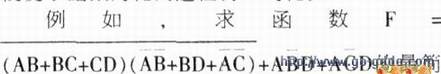
　　与或式，传统的解题方法是先求该函数的与或或，再利用卡诺图进行化简，其过程如下：

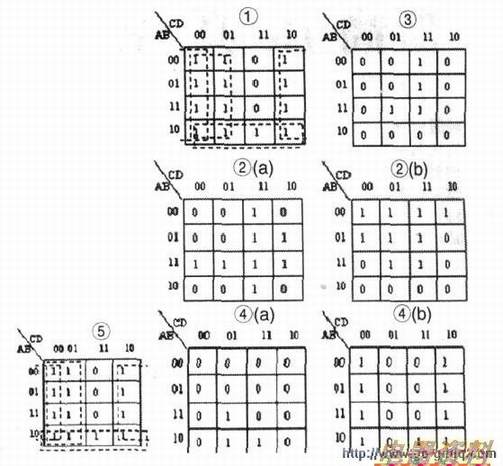
　　该函数的卡诺图如图l所示。

　　由卡诺图化简函数，可得该函数的最简与或或：F=C+D+AB对于这个例子，我们可以将复杂函数分解成多个逻辑函数的逻辑运算，然后通过卡诺图对函数进行运算，从而求出复杂函数的卡诺图，最后对该卡诺图进行化简得到逻辑函数的最简与或或。其过程如下：我们设FI=AB+BC+CD,F2=AB+BD+AC.F3=ABD+ACD若设F4=F1.F2,则有F=F4+F3Fl和F2的卡诺图如图2(a)、(b)所示，由该两函数的卡诺图进行与运算，便得到函数F4的卡诺图，如图3所示。F3的卡诺图如图4(a)所示，由F4的卡诺图可得F4的卡诺图如图4(b)所示，由该两函数的卡诺图进行或运算，便得到函数F的卡诺圈．如图5所示。

　　由F的卡诺图，可得函数F的最简与或或为：

　　从以上两种解题方法可以看到，利用卡诺图进行逻辑运算既简洁、直观、不易出错，又大大简化了该题的求解过程。