◆ z变换在离散系统中的作用,与拉氏变换在连续系统中的作用非常相似。 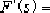 | £ | 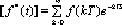 |
若设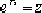 ,并将 ,并将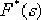 写成F(Z),则得 写成F(Z),则得
F(z)就叫做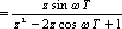 的z变换,并且以 的z变换,并且以 表示 表示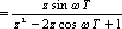 的z变换。 的z变换。 在z变换中,只考虑采样时的信号值。因此,f(t)的z变换与f*(t)的z变换有相同的结果。即:
因为F(z)只取决于f(t)在t=kT(k=0,1,2,…)上的数值,所以F(z)的z反变换,只给出了f(t)在采样瞬间的信息。 表7-1列出普通时域函数的z变换,表7-2列出z变换的常用性质。
| | X(s)
| x(t)或x(k) | X(z) | | 1 | 1 | δ(t) | 1 | | 2 | e
-kTs | δ(t-kT) | z-k | | 3 | 1/s | 1(t) | z/(z-1) | | 4 | 1/s2 | t | Tz/(z-1)2 | | 5 | 1/(s+a) | e -at | Tz/(z-eaT) | | 6 | a/(s+a) | 1-e -at | (1-eaT)z/[(z-1)(z-eaT)] | | 7 | ω/(s2+ω2) | sinωt | zsinωT/(z2-2zcosωT+1) | | 8 | s/(s2+ω2) | cosωt
| z(z-cosωt)/(z2-2zcosωT+1) | | 9 | 1/(s+a)2 | Te-at | TzeaT/(z-eaT)2 | | 10 | ω/[(s+a)2+ω2] | e-atsinωt | zeaTsinωT/(z2-2ze-aTcosωt+e-2aT) | | 11 | (s+a)/[(s+a)2+ω2] | e-atcosωt
| (z2-zeaTcosωT)/(z2-2ze-aTcosωt+e-2aT) | | 12 | 1/s2 | t2 | T2z(z+1)/(z-1)2 | | 13 | | ak | z/(z-a) | | 14 | | akcoskπ | z/(z+a) |
7.3.2 z变换的方法 ⒈级数求和法
举例说明之。
例7-1 求单位阶跃函数1(t)的z变换 注意:只要函数z变换的无穷级数F(z),在z平面某个区域内收敛,则在
应用时,就不需要指出F(z)的收敛域。
例7-2 求下列函数的z变换........ f(t)=0(t<0)
f(t)=eωt(t≥0) 解: 例7-3 求下列函数的z变换........ f(t)=0(t<0)
f(t)=sinωt(t≥0) 解:
⒉部分分式法
当给定某连续函数f(t)的拉氏变换F(s)时,欲求其z变换,可利用本法,因为许多函数F(s)利用部分分式可以化成如下形式: 通过其中的每一项拉氏反变换得到原函数f(t)为: 而其z变换可以表示为: 下面举例说明。 例7-4 求下列函数的z变换:F(s)=1/s(s+1) 解: 先将F(s)展开成部分分式。 其中, 1/s[或1(t)]相应的z变换为z/(z-1) ,而1/(s+1)[即e-t] 相应的z变换为
z/(z-e-T) | 则: | 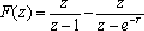 | 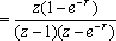 |
| | x(t)或x(k) | Z[x(t)]或Z[x(k)] | | 1 | ax(t) | ax(z) | | 2 | x1(t)+x2(t) | X1(z)+X2(z) | | 3 | x(t+T)或x(k+1) | zX(z)-zx(0) | | 4 | x(t+2T) | z2X(z)-z2x(0)-zx(t) | | 5 | x(k+2)
| z2X(z)-z2x(0)-zx(1) | | 6 | x(t+kT) | zkX(z)-zkx(0)-zk-1x(T)- …-zx(kT-T) | | 7 | x(k+m) | zmX(z)-zmx(0)-zm-1x(T)- …-zx(m-1) | | 8 | tx(t)
| 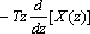 | | 9 | kx(k)
| 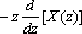 | | 10 | e-atx(t) | X(zeaT) | | 11 | e-akx(k) | X(zea) | | 12 | akx(k) | x(z/a) | | 13 | k akx(k) | 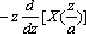 | | 14 | x(0)
| 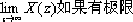 | | 15 | x(∞)
| 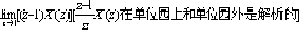 | | 16 | 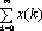 | x(1) | | 17 | 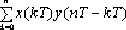 | X(z)Y(z) |
|