从实例中学习OrCAD-PSpice10.3-AA(蒙特卡洛工具)

 

　 PSpe 一直重视所设计的，要能适合于批量生产的需要。现在PSpice10.3单独设立MonteCarlo工具，使这一项工作得到加强。本章先简介容差分析的基本概念，其后重点介绍MonteCarlo工具的使用方法。

　　6.1容差分析

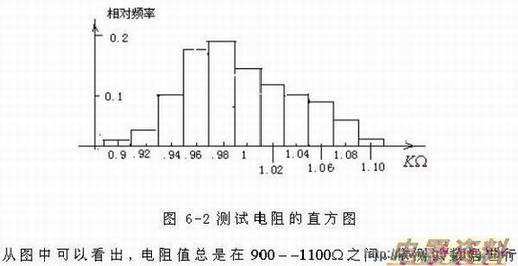
　前几章所述电路分析法时，已经提过只将元件视作理想元件按标称值进行分析是不全面的。实际上，由于生产工艺的不同或老化等原因，元件值与理想元件值（称为标称值）之间，都存在一定的偏差。比如，标为1kΩ的，如果偏差为±10%，那么实际元件值可能是在1.1kΩ～900Ω之间的某一值。设计者不仅需要分析当电路元件为标称值的电路响应，还需分析当电路元件值在一定范围内变动时电路响应所发生的变化。所谓容差分析就是研究元件参数值的变化（公差）对电路特性的影响（公差）；或者相反，由给定的电路特性的公差，求元件参数值的公差。一般来说，保证电路在性能指标范围内，尽可能地扩大元件的容差范围以便降低成本，这是设计者几乎天天必须考虑的问题。

　　6.2 蒙特卡洛 （MonteCarlo简写为MC）法< /p>

　前面关于电路参数灵敏度的计算，反映了电路参数的改变对电路特性影响的大小，这对设计人员来说无疑是重要的。然而很多情况下，并不能确切知道各个参数的实际改变量，而只是知道各个参数的随机分布规律或者是变化范围。在这种情况下，怎样来分析电路特性的随机分布规律或者它的相应变化范围，这就是容差分析所要讨论的问题。由于这种不确定性，容差分析一般用概率统计分析，而且多用蒙特卡洛法。

　在计算机上进行蒙特卡洛分析时关键在于用计算机产生随机数。然后用一组一组的随机数对各元件取值。元件的分布规律有：

　1.均匀分布(FLAT)

　任一元件值在容差的上下限范围内以相等的概率出现，该类元件值为均匀分布。又因其元件偏差和出现图为距形，所以也称距形分布，实际上，这种分布是很少的，因为它很简单。PSpice中用“DIST”设置元件值的分散性其默认值就是FLAT。

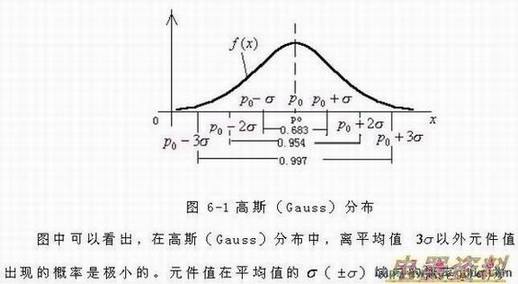
　2.正态分布或称高斯（GAUSS）分布（常用）