三极管栅极-板极特性曲线

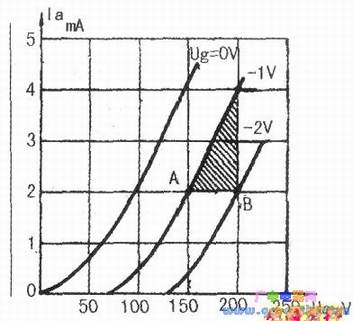
　对二极电子管而言只有两个主电极，其板流特性亦取决于板压（特殊用途除外）。所以，其板流特性曲线即由板流构成Y轴，板压构成X轴的伏安特性。三极管加入控制栅极以后，板极既受板压控制，同时也受到栅极电位控制，为了同时反映出两电极对板流的影响，常用的表示方法是在类似二极管的板压一板流坐标图中，以不同的栅极电位为基准，列出多条板压一板流特性曲线，构成所谓栅压一板极特性曲线族，通常写作Ug(Ua-Ia)特性曲线族。下图所示为三种不向Ug值的Ug(Ua-Ia)特性曲线，在此曲线中，可从X、Y轴中读出Ug从0V到-2V，板压从0V～250V的任意点所对应的板极电流值。例如下图的A点，表示当板压=150V（A点作为垂直线与X轴的交点电压值），栅压Ug=-lV（曲线标准值1时，A点作水平线与Y轴相交的点2mA，即为此状态的板流值。  

　当以Ug=-lV为基准取任何一点在XY轴上读出Ug、la值，均为Ug=-lV时板压所对应的板流值。如果将Ug曲线间距离行等分的量化，不难做出Ug=-lV的1/2直到1/10，从而描绘出Ug=-0.5V，甚至Ug=-1.1V～1.9V任何值的曲线。只要描绘的新曲线与前后曲线各点间保持等距离（可理解为平行的曲线），其误差可在电子管参数误差范围之内。以此方式在特性曲线坐标图上很容易读得在一定范围内Ua、Ug值所对应的板极电流。

　除了直接读取任意条件下的板流以外，如果对板流进行多种状态的读出，还可以得到板流变动的趋势，以了解在预定的板压时，栅极电压变动范围所导致的板流变动是否在板流饱和点和截止点之间的线性区内，作为保证实现高保真放大的必须条件。例如在下图中，显然当板压Ua=150V时，只要Ug在-2V以上，板流已趋截止，而按三极管A类放大的惯例，在Ug=0V时板流为最大，其值不应超过板流极限的允许值（此关系在工作点选择一节中已有详述，可参考）。

　另外，在Ug(Ua-Ia)特性曲线族中还可以通过简单的作图和算术运算，得出该电子管的三项基本参数：

　跨导S、内阻Ri和电压大系数μ。为此，首先介绍跨导S的求法，根据跨导的定义，是指板压不变时，栅压Ug对板流Ia的控制能力，写成算式即S=△Ia/△Ug。其意义为板压不变时板流Ia的变量与栅压Ug变量之比。

　其结果意味着栅压变动1V时，引起多少mA的板流变动（此时跨导单位为mAN，又称为微姆欧写成M，也有的国家称为微模）。显然，S越高的管子栅极对板流的控制能力越强，每1V栅压变动将引起更大板流变动。根据上述定义，可在下图Ug(Ua—la)特性曲线族中找出两个点，此两点位于坐标图中同一垂直线上，因而两点在x轴（表示板压Ua）上的投影点是重合的，意味着此两点代表板压Ua是相等的，同时将此两点选择在不同的Ug特性曲线上，则完全符合跨导的测试要求（如下图的B和C点）。由图中可读出B点对应X、Y轴的数据X轴Ua=200V，Y轴Ia=2mA，此时Ug=-2V，C点位于Ug=-lV的曲线上，其Ua同样为200V，但Ia升高到4mA，由此根据S定义：

　　1V的应用状态跨导值，实际上S值随电压状态有所变化，在应用电压值下求得S是比较接近应用实际S的。

　　从特性曲线族中也可方便地求出电子管板极内阻Ri，根据Ri定义，为板极电压变量对板流变量之比，写成算式则Ri=△Ua/△Ia，为了不涉及栅压Ug对板流的控制作用，求得的内阻Ri显然需在Ug不变的条件下进行。为此，，在Ug=-lV的曲线上再选择一点A，所以Ug=-lV的情况下改变Ua，以观察Ia变动结果。显然，A点数据为Ug=-1V，Ua=150V，la-2mA，而C点数据为Ug=-lV，Ua=200V，Ia=4mA，根据Ri定义，单纯Ua变动150V～200V，引起la变动为2mA～4mA，代入公式Ri=△Ua/△Ila=(200-150)V/2mA=25kΩ，即为此管在Ug=-1V时板极内阻。

　　求得S、Ri以后，根据电子管三项基本参数的关系：S×Ri=μ，可求的该管电压放大系数μ，当S单位为mA/A时，Ri单位相应为kΩ。