节点电压法在电路系统分析方法中的应用

　节点法是的系统分析方法之一，所谓节点电压是指电路中任一节点与参考节点之间的电压，该电路分析方法的本质是先利用KVL疋理将各支路用节点电压表示，然后只列n-1各节点的KCL方程（n为所分忻电路的节点数）。支路电流法既列KVL方程又列KCL方程，回路电流法只列KVL方程。与这两种电路分析方法相比，当电路的节点数转少，支路数较多时，采用节点电压法简单，因为列的方程数较少。特别是当有理想电压源直接并接在两节点之间时，只要灵活应用节点电压法。便可以进一步减少所列的方程数。  

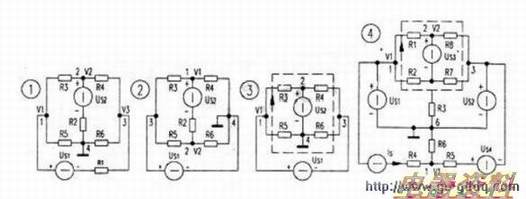
　图1中有4个节点，选4为参考节点的话，1、2、3节点的节点电旺分别没为Vl、V2、V3，列出三个节点的KCL方程分别为：（1/R1+1/R3+1/R5）V1一1/R3V2一1/R1V3=Us1/R1（节点1）：-l/R3V1+（1/R2+1/R3+1/R4）V2-1/R4V3=Us2/R2（节点2）；-1/R1Vl-1/R4V2+（1/R1+1/R4+1/R6）V3=-Us1/R1（节点3）。

　当有一个理想电压源直接并接在两节点之间时，一般选电压源的负极为参考节点，则电压源的正极所在节点的节点电压就是这理想电压源的值。为已知的，可少列一个KCL方程。图2中同样有4个节点，理想电压源Us1直接并接在两节点之间，选其负极昕在的节点4为参考节点，则正极所在的节点3的节点电压为Us1已知，只需设节点1、2的节点电压V1、V/2为未知量，列KCL方程也只需列两个。选节点列KCL方程时要避开有理想电压源直接并接的支路，因为电压源中流过的电流由外电路决定，不能用所没未知量节点电压来表示。若要列出含有理想电压源支路的节点（图2中的节点3）的KCL方程。则需增设该支路电流为未知量。故选取1、2节点分别列KCL方程为：（1/R2+1/R3+1/R4）V1-1/R2V2=Us2/R2+Us1/R3：一1/R2V1+（1/R2+1/R5+1/R6）V2=Us1/R5一Us2/R2。两个未知量两个方程程。不需要列节点3的KCL方程。

　当有二个或以上理想电压源直接并接在节点之间时，如果这些电压源共负极，选负极为参考点，不共负极时。任选一的负极为参考，占。图3中还是有4个节点，本来要设3个未知量，但有2条理想电吐源直接并接的支路，故只需设一个未知量，选好4为参考节点后，设节点l的节点电压V1为未知量，节点2的节点电压为电压源的值Us2节点3的节点电压为V1一Us1。只需列一个KCL方程。但l、2、3三个节点都含有理想电压源直接并接的支路，要列KCL方程必须增设这些支路的电流为未知量。

　所以不想增加未知量与方程的个数的话，可以灵活应用KCL定理的推广形式：选取虚线所在的面列面的KCL方程，该而交割了4条支路，但避开了理想电压源直接并接的支路，KCL方程为：（V1一Us2）/R3+（V1-Us1-Us2）/R4+（V1一Us1）/R6+V1/R5=O.整理后为：

　（1/R3+1/R4+1/R5+1/R6）V1=（1/R4+1/R6）Us1+（1/R3+1/R4）Us2.

　图4中有6个节点，本来要设5个未知量，列5个KCL方程，但有3个理想电压源直接并接在两节点之间，只需设2个未知量，Us1、Us2的负极都连接在节点6上，故选其为参考节点，分别设1、2节点的节点电压V1、V2为未知量，4、5的节点电压分别为Us1、Us2,3的节点电压为V2-Us1。要选两个节点列KCL方程。只有节点1不含有理想电压源直接并接的支路，其KCL方程为：（1/R5+1/R6）V1=Is+Us2/R5+Us4/R5，另一个KCL方程只能选取一个面（该面同样下要交割到有理想电压源的支路）来列，如图中虚线所示：（Us1—V2）/R1+（Us2-V2）/R8+（Us2一V2+Us3）/R7+（Us1一V2+Us3）/R2+（O-V2+Us3）/R3=O，整理后为：（1/R1+1/R2+1/R3+1/R7+1/R8）V2=（1/Rl+1/R2）Us1+（1/R7+1/R8）Us2+（1/R2+1/R3+1/R7）Us3。