运用综合法化简逻辑函数
一、化简逻辑函数的一般方法
一般化简逻辑函数的方法有两种,一是公式法,二是卡诺图法。公式法比较复杂。包括并项法、吸收法、配项法、消去法等。
因为其依据的公式有几十个。而且并不都能直接应用公式。很容易出错。这种方法的优点是任何逻辑函数的运算都可以用公式法进行化简。
另一种方法是图形法。也就是卡诺图法,这是比公式法要直观和简单得多的方法。优点是能够通过卡诺图找出直接运用逻辑函数化简公式,较方便地把逻辑函数化简。
二、逻辑函数的综合化简法
所谓“综合”就是综合了公式法和卡诺图法优点的一种逻辑函数化简方法,这种方法是把逻辑函数的化简变成了数的运算,所以简单,并且化简出来的结果比较标准化。这也有利于计算机的生产。
综合化简法的原理是充分运用化简逻辑函数的定律和电路的基本特点来确定的。比如说。在逻辑函数的运算中A+A=l。而在实际电路中,A+A的实际意义就是相互抵消了,这一项不存在。所以这种综合化简逻辑电路是符合实际的。
在应用这种方法前。要搞清两大问题:
一是逻辑函数变量和常量的关系问题。我们知道:A=1,而A=0。
那么在一组逻辑函数中就可以根据“是”或“非”来将变量转化为二进制的数字了。比如。ABCD=101l。
ABCDE=01001,以此类推。再将这些用二进制数字表示的逻辑函数进行“运算”,从而求出其逻辑函数的“和”,这个“和”就是相应逻辑函数的化简。
二是化简逻辑函数遵守的运算规则:第一是1+1=1。第二是0+0=0,第三是l+0不存在。第一和第二易于理解,符合二进制加法原理的。
但是第三的1+0为不存在,就不好理解了。其实l+0就是A+A的表示,这个问题也不难理解。前面已经说过,化简逻辑函数是为了减少相关的逻辑电路。在电路中,A代表一个原电路,A代表这个电路的“非”
电路,而这样的两个电路组合在一起时,其结果是这两个电路的作用功能互相抵消了,因此相当于这两个电路都不存在了,也就是这两个电路被“化简”掉了。
三、运用综合法化简逻辑函数
下面主要介绍三变量和四变量逻辑函数的化简,其他变量的化简方法可由此而推广。
1.三变量逻辑函数的化简首先,我们把三变量的逻辑函数放在三变量的卡诺图中。卡诺图是解决现实问题中的一个必要条件,一个实际问题提出后,首先是把逻辑关系用真值表表示出来。再在真值表的基础上画出卡诺图。所以任何实际问题都必须要把逻辑函数在卡诺图中画出来,然后再进行化简。画卡诺图是化简逻辑函数必不可少的一个步骤。
 则计算式如下:
则计算式如下:
 我们这里是讲方法。所以开始好像还比公式法复杂些,一旦学会了后,这个方法就简单了。
我们这里是讲方法。所以开始好像还比公式法复杂些,一旦学会了后,这个方法就简单了。

计算:按规则![]() 101,则计算如下:
101,则计算如下:

2.四变量逻辑函数的化简
例1:计算:![]()
卡诺图如下:

例2:计算:![]()
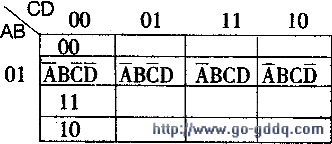
计算: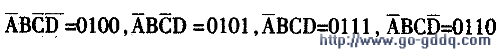

这个综合方法十分简单,其依据的原则是符合逻辑函数和逻辑电路规则的,结果是准确的。
- 上一篇:浅谈扬声器与音箱配合设计
- 下一篇:同轴线Coaxial