三个重要的等式规则
在逻辑代数中,利用代入规则、对偶规则、反演规则可由基本定律推导出更多的公式。
1. 代入规则
在任何一个逻辑等式中,如将等式两边所有出现某一变量的地方都用同一函数式替代,则等式仍然成立。这个规则就是代入规则。
代入规则扩大了逻辑等式的应用范围。
例如 已知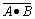 =
=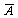 +
+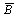 ,如用B·C来代替等式中的B,则等式仍成立,故有
,如用B·C来代替等式中的B,则等式仍成立,故有
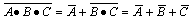
2. 对偶规则
将某一逻辑表达式中的"·"换成"+"、"+"换成"·" ;"0"换成"1","1"换成"0",就得到一个新的表达式。这个新的表达式就是原表达式的对偶式。如果两个逻辑式相等,则它们的对偶式也相等。这就是对偶规则。
例1114 已知A+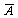 B=A+B,求其对偶式。
B=A+B,求其对偶式。
解:利用对偶规则,可得到A·(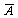 +B)=AB。
+B)=AB。
3. 反演规则
如将某一逻辑式中的"·"换成"+"、"+"换成"·" ;"0"换成"1","1"换成"0" ;原变量换成反变量,反变量换成原变量,则所得到的逻辑表达式称为原式的反演式。这种变换方法称为反演规则。利用反演规则可以比较容易地求出一个函数的反函数。
例1115 求函数y=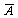 ·B+C·
·B+C·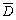 +0的反函数。
+0的反函数。
解:利用反演规则可得: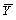 =(A+
=(A+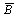 )·(
)·(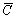 +D)·1
+D)·1
例1116 证明加法对乘法的分配律:A+BC=(A+B)(A+C)
证: (A+B)(A+C)=AA+AC+AB+BC
=A+AB+AC+BC (重迭律)
=A(1+B+C)+BC
=A+BC (0 -1律) (证毕)
例1117 求证A+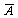 B=A+B
B=A+B
证:A+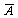 B =(A+
B =(A+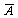 )(A+B) (加法对乘法的分配律)
)(A+B) (加法对乘法的分配律)
=1·(A+B) (互补律)
=A+B (0-1律) (证毕)
例1118 己知Y=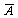 (B+C
(B+C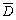 )+
)+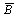 C,求
C,求
解: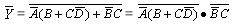
=(A+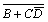 )(B+
)(B+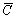 )=(A+
)=(A+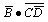 )(B+
)(B+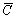 )
)
=[A+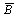 (
(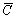 +D)](B+
+D)](B+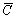 )
)
若运用反演规则,可直接求出: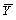 =[A+
=[A+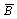 (
(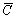 +D)](B+
+D)](B+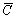 )
)
S如前所述,逻辑函数有多种表示法,它们之间可以相互转换。
1. 代入规则
在任何一个逻辑等式中,如将等式两边所有出现某一变量的地方都用同一函数式替代,则等式仍然成立。这个规则就是代入规则。
代入规则扩大了逻辑等式的应用范围。
例如 已知
2. 对偶规则
将某一逻辑表达式中的"·"换成"+"、"+"换成"·" ;"0"换成"1","1"换成"0",就得到一个新的表达式。这个新的表达式就是原表达式的对偶式。如果两个逻辑式相等,则它们的对偶式也相等。这就是对偶规则。
例1114 已知A+
解:利用对偶规则,可得到A·(
3. 反演规则
如将某一逻辑式中的"·"换成"+"、"+"换成"·" ;"0"换成"1","1"换成"0" ;原变量换成反变量,反变量换成原变量,则所得到的逻辑表达式称为原式的反演式。这种变换方法称为反演规则。利用反演规则可以比较容易地求出一个函数的反函数。
例1115 求函数y=
解:利用反演规则可得:
例1116 证明加法对乘法的分配律:A+BC=(A+B)(A+C)
证: (A+B)(A+C)=AA+AC+AB+BC
=A+AB+AC+BC (重迭律)
=A(1+B+C)+BC
=A+BC (0 -1律) (证毕)
例1117 求证A+
证:A+
=1·(A+B) (互补律)
=A+B (0-1律) (证毕)
例1118 己知Y=
解:
=(A+
=[A+
若运用反演规则,可直接求出:
S如前所述,逻辑函数有多种表示法,它们之间可以相互转换。
- 上一篇:逻辑代数的基本定律
- 下一篇:由逻辑表达式求真值表